こんにちは。14期のbayashiです。この記事はデジクリアドベントカレンダー14日目の記事となります。
まずはこれを聴いて欲しい
※やや大きな音がします
DAWのループMIDI素材から持ってきたピアノフレーズを2回、あるエフェクトの有無だけを変えて再生してみました。
2つのフレーズを聴き比べると、初めは音楽室等で聴くような普通の音で、2つ目は大きなホール等で聴くような響きのある音だったと思います。
このように残響効果を加えるエフェクトを「リバーブ」と呼びます。
エフェクタとしてのリバーブはヤマハのここのページが非常にまとまった説明をしているので気になる方は見てみるといいでしょう。
コンボリュージョンリバーブと畳み込み
リバーブの種類のひとつに「コンボリュージョンリバーブ」と呼ばれるものがあります。これは現実世界の建物等で計測した残響のデータから残響効果を生み出すリバーブで、冒頭の動画で使ったリバーブもこのタイプです。
コンボリュージョン(Convolution)とは「畳み込み」という計算を指す言葉で、この種のリバーブは残響を作り出す過程で畳み込みの計算をしています。
その畳み込みですが、定義式はこのようなものです。
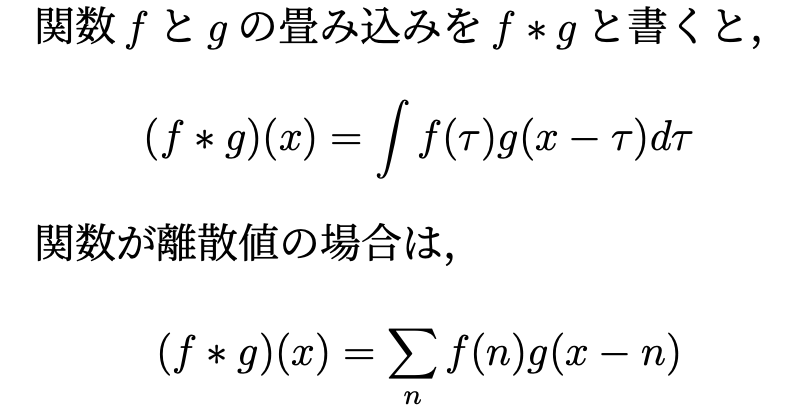
「ずらして掛けて足し合わせる」という何やら不思議な計算に見えますね。
この「畳み込み」という計算、理学・工学の割といろんな場面で出てくるのですが、定義式から何をする計算なのかイメージし辛く結構な初見殺しポイントではないかと感じています。
そこで今回、色々あって「コンボリュージョンリバーブの仕組みから良い感じに畳み込みを説明出来そうな気がする…!」と思い立って、記事を書いてみることにしました。
この記事ではコンボリュージョンリバーブによる残響の畳み込みを題材に、畳み込みが「結局どんな計算なのか」について書いていきたいと思います。
コンボリュ(以下略)の仕組み
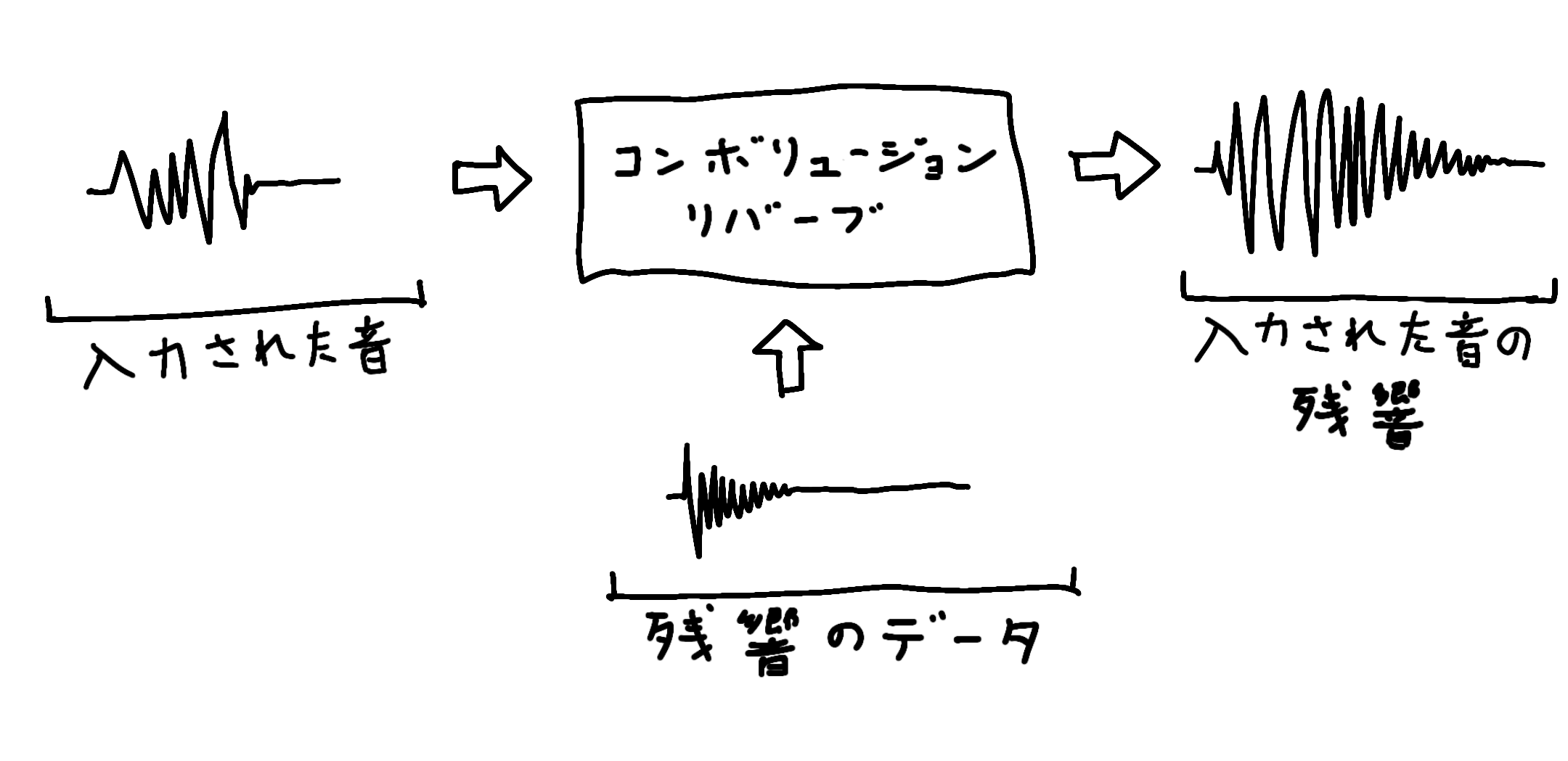
※図中のゴニョゴニョは「音の波形」…のつもりです…
まず全体像として、コンボリュージョンリバーブは「入力された音」と「残響のデータ」を合成して「入力された音の残響」を出力します。(実際のエフェクトでは出力に元の音を一定の割合混ぜています。)
「残響のデータ」というのは、簡単に言えば「ある一瞬の音がどのように残り、消えていくのか」を記録した音声です。詳しくは触れませんが、イメージとしては「音がよく響く静かな場所で一発パチンと手を叩いたときに残る音」を記録したようなものだと思ってください。
冒頭の動画で使った「残響のデータ」を再生するとこのようになります。
※やや大きな音がします
残響の畳み込み
この「入力された音」と「残響のデータ」を合成する工程こそが何を隠そう畳み込みです。
この工程で行われる畳み込みの計算を、ここでは次のように考えます。
(扱う信号は離散値、つまりディジタルである前提です。)
- 入力された音の波形をめっちゃ拡大すると「ある瞬間の振幅の値(サンプル)が順に連なっている」形になっています。
- そのサンプル一つ一つを取り出して、それぞれ「残響のデータ」と掛けます。これで「一つ一つのサンプルから発生する残響」が得られます。
- それぞれのサンプルから発生する残響たちを順に重ね合わせます。
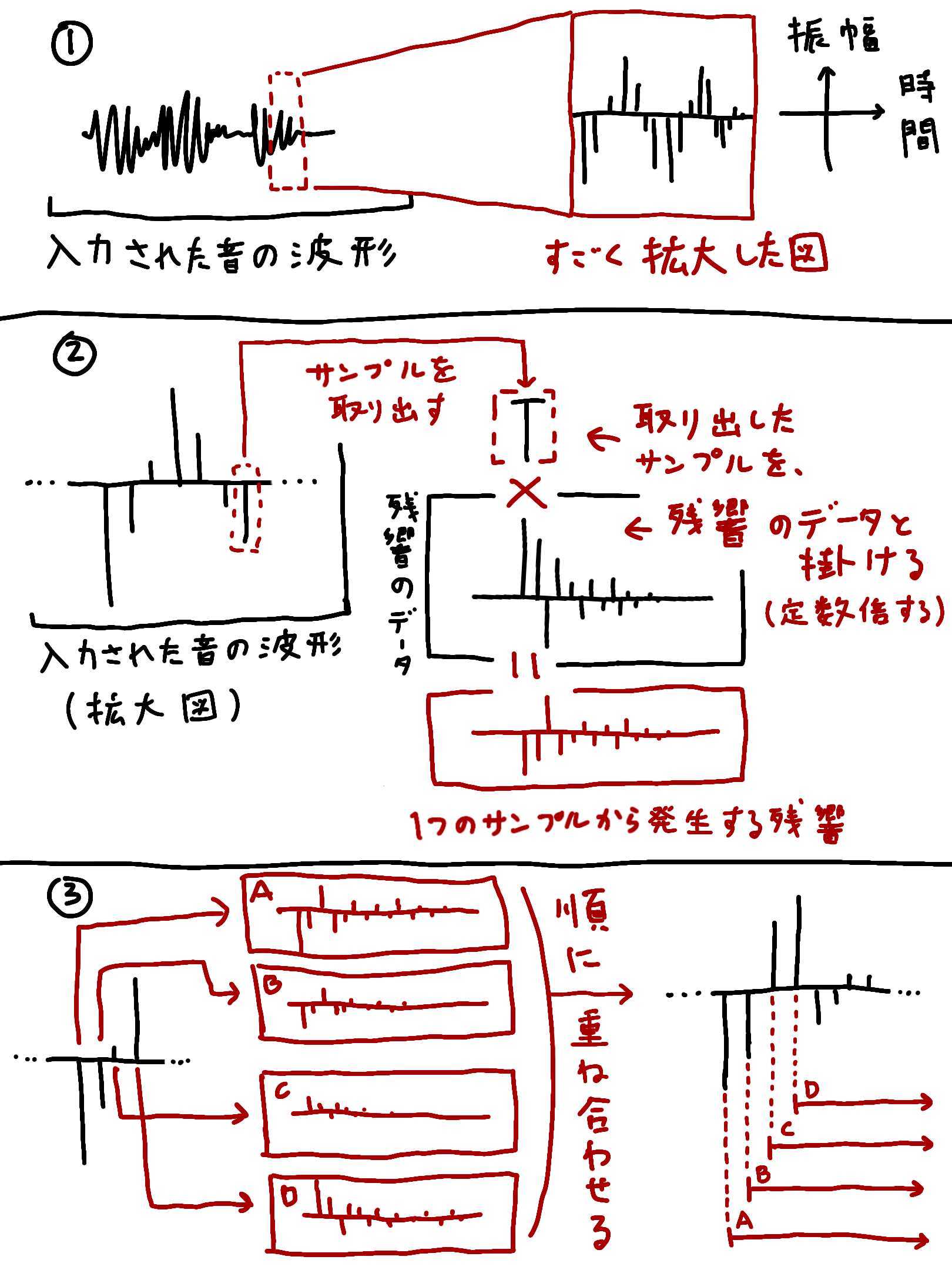
これで計算完了です。
つまるところ、ここでやっているのは、
「一瞬の音ごとに残響を発生させる」&「それぞれから発生した残響どうしを重ね合わせる」
という簡単なお仕事です。
数式上で確認してみる
では、今やったことを数式として表現してみましょう。
まず、ここでは次のように音の波形を「関数」として表します。

※追記 : 離散値の信号を表すときは普通の括弧()ではなく角括弧[]を使うことが多いのですが、執筆当時あまり意識していなかったため数式は普通の括弧で書いています。m(__)m
例えば、入力された音の位置 x=0 のサンプルを取り出して、そのサンプルと残響のデータを掛ける様子はこのように表現できます。(取り出したサンプルの位置が分かるように、関数 h の右下に数字を添えておきます。)
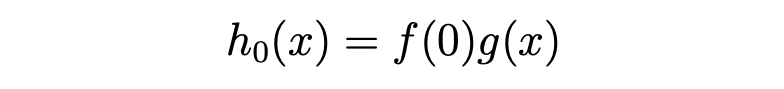
これは「位置 x=0 のサンプルが発生させる残響」と捉えることができます。
同じように x=1, x=2, ..., x=n から取り出したサンプルが発生させる残響もこのように書けます。
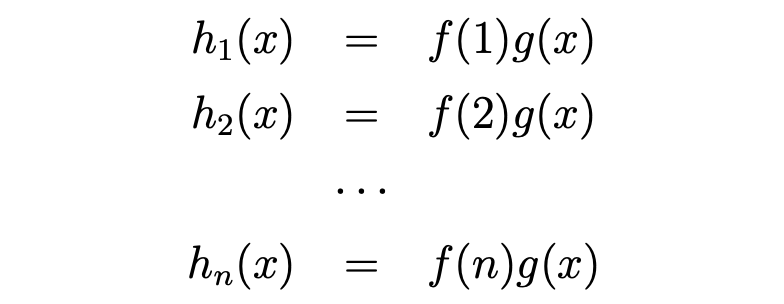
では、これらを順に重ね合わせていきます。それぞれ取り出したサンプルの位置が残響の起点となることに注意して、次のように書けます。(スマホの方は細かくなってしまってすみません…)
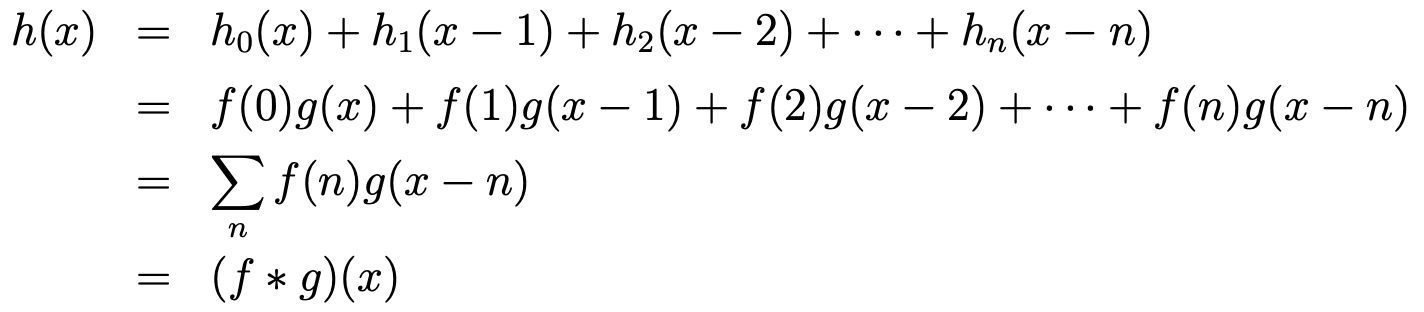
それをスマートな形にまとめると、あの序盤に書いた定義式が出てきます。
ということで、以上が「畳み込み」の計算です。
まとめ
畳み込みでやっている計算は、
- 片方の関数の値を固定して、もう片方の関数と掛ける
- それを(固定する関数の)全ての値に対してやる
- その結果を互いに重ね合わせる
…と考えることが出来ます。
定義式の通り「片方の関数をずらしながら和をとる/積分する」と捉えるのも勿論正しいですが、離散値を扱う場合は上記の解釈の方が直感的に考えやすいかと思います。
その他(余談と補足)
今回「残響のデータ」は「ある一瞬の音がどのように残り、消えていくのかを記録した音声」だと書きましたが、信号処理の文脈ではこのような「一瞬の信号に対する反応」のことを「インパルス応答(Impulse Response : IR)」と呼びます。
さらに、一定の条件(出力が歪んでいない等)が満たされている場合、
インパルス応答が分かっているとき、それと入力信号を畳み込むと出力信号が分かる
…という性質が成立します。
畳み込み計算はいろんな分野にいろんな役割で登場する…と何度か書きましたが、
例えば画像処理なら、輪郭強調やノイズ除去に使われる「フィルタ処理」に2次元の畳み込み計算が使われます。
「一瞬の信号に対する反応を…」みたいな用途ではありませんが、計算手順は今回と同じような解釈で捉えることが出来ます。
その他工学系だけでなく理学系でも畳み込み計算は現れるようです。
あとがき
何というか思いつきで需要が謎すぎる記事を書いてしまいました。
私は「授業で習った謎の計算が実は身近なところで使われていた…!」みたいなのが結構好きなので、普段使っているリバーブと畳み込みの関係に気付いたときは結構興奮しました。
兎に角、こんな記事をここまで読んでくださって本当にありがとうございました!
今度はDTMの記事を書きます。多分。
業務連絡
現在(12/14 2:15)、明日の記事はまだ登録されていません。
技術でも趣味でも、推し語りでも日記でも、今期見ているアニメのことでも、
何か書きたい!という方は是非気軽に参加してみましょう。